
工業簿記ではシュラッター図などグラフを用いた問題が出題されますが、問題を解くには一次関数とそのグラフの知識が必要です。
中学で学ぶレベルの数学ではありますが、案外むずかしいもの。
シュラッター図や損益分析が苦手な方や、「一次関数?細かいところ忘れちゃった」「今さら人に聞けない」という方には、この記事がお役に立てると思います。
一次関数とグラフ
一次関数とはどういうものか、そのグラフの特徴について説明します。
一次関数とは
りんごを購入するときの個数と値段について考えてみます。
1個100円のりんごを10個買うときの値段は?
100×10=1,000円ですね。
では、その2倍の20個買うときの値段は?
100×20=2,000円です。
3倍の30個買うときの値段は?
100×30=3,000円です。
このりんごを買うときの「個数と値段」のように、片方を倍にすればもう片方も同じように倍になる、片方を3倍にすればもう片方も3倍になる、というような関係を「比例」と言います。
では次のケースを考えてみましょう。
りんご(@100円)を購入する際に送料が500円かかる(個数がいくつでも)とした場合はどうなるでしょうか。
10個買う場合は、100×10+500=1,500円
20個買う場合は、100×20+500=2,500円
30個買う場合は、100×30+500=3,500円
個数が倍になっても値段は倍になっていませんし、個数が3倍になっても値段は3倍になっていません。
これは比例ではありません。
しかし増分に注目してみます。
個数が10個⇒20個のとき、
個数の増分:10個、値段の増分:1,000円。
個数が10個⇒30個のとき、
個数の増分:20個、値段の増分:2,000円。
個数の増分が倍になったとき、値段の増分も倍になっています。個数の増分が3倍になったとき、値段の増分も3倍になっています。
この増分どうしが比例している関係を「一次関数」といいます。
一次関数とは
一次関数とは、ある量XとYが以下の関係にあることをいいます。
Y = a × X + b (a, bは定数)
先程の例では、りんごの個数をX、値段をYとすると(りんごの単価100円、送料500円)
Y = 100 × X + 500
となっているので、個数と値段は一次関数の関係にある、といいます。
一次関数では、Xの増分とYの増分は「比例」の関係があります。
なお、送料がない場合は、
Y=100 × X
となりますが、定義の式でb=0の場合の形になるので、これも一次関数です。比例は一次関数の特殊な場合(b=0)になります。
グラフの傾きと切片
一次関数をグラフで表してみましょう。
横軸(X軸)にりんごの個数、縦軸(Y軸)に値段をとって、グラフを書いてみます。
個数が10の場合は値段は1,500 ⇒ (X,Y)=(10, 1500)
個数が20の場合は値段は2,500 ⇒ (X,Y)=(20, 2500)
個数が30の場合は値段は3,500 ⇒ (X,Y)=(30, 3500)
とグラフ上に点を打って点どおしを結ぶと、以下のようなグラフになります。

傾きとは
1次関数のグラフにおいて、
(Yの増分)/(Xの増分)
のことを傾きといいます。
あるいは変化率とも言ったりします。
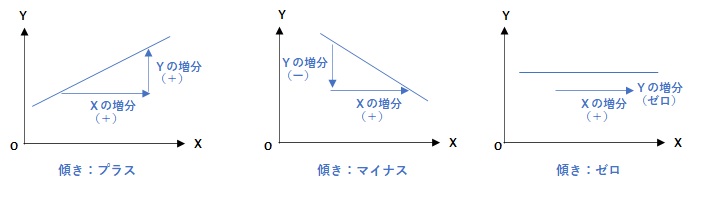
グラフのかたちと傾きには以下のような関係があります。
- グラフが右肩上がりのとき:傾きはプラス(Xの増分がプラスのときYの増分もプラスになるから)
- グラフが右肩下がりのとき:傾きはマイナス(Xの増分がプラスのときYの増分はマイナスになるから)
- グラフが水平のとき:傾きはゼロ(Yの増分は常にゼロだから)
そして、次が大事な点ですが、
Y= a × X + b のグラフの傾きは a
になります。
先程のりんごの例を見てみます。
グラフは以下の2点を通っています。
(X,Y)=(10, 1500)(→点Aとする)
(X,Y)=(20, 2500)(→点Bとする)
点Aから点Bに変化したときに、
Xの増分は、20 - 10 = 10
Yの増分は、2500 - 1500 = 1000
となるので、
傾き =(Yの増分)/(Xの増分)= 1000/10 = 100
となります。aと一致していますね。
これを一般的に示します(ちょっと難しいですが)。

切片とは
一次関数のグラフにおいて、グラフ(直線)がY軸と交わる点を切片といいます。
りんごの例でいうと切片は500になります。
一般的に、
Y= a × X + b のグラフの切片は b になります。
なぜなら、Y軸の上にある点の X は 0 なので、Yは、
Y = a × 0 + b =b
となります。よって、切片は b となります。
以上が一次関数とグラフの主な特徴です。
工業簿記での使い方
一次関数やそのグラフの応用範囲は広いですが、ここでは工業簿記に出てくるシュラッター図と固変分析について、使い方を説明します。
シュラッター図
シュラッター図とは、操業度と費用の関係を図(グラフ)にしたものです。
費用は、固定費部分と変動費部分に分かれます。
そして変動費は、変動費率×操業度 になります。
したがって、
費用=変動費率×操業度+固定費
の関係があります。
費用をY、操業度をX、変動費率をa、固定費をb、とすれば
Y= a × X + b
の関係が成り立っています。
つまり、費用と操業度は一次関数の関係にあります。
これを理解していればシュラッター図は簡単です。
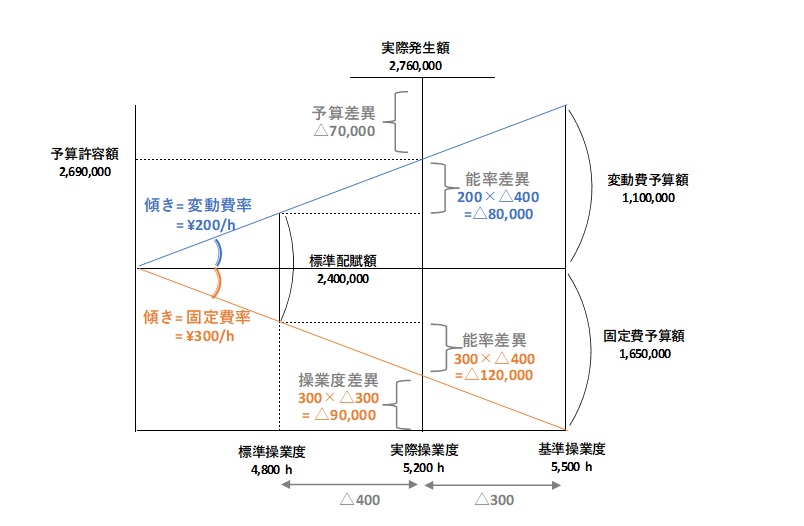
シュラッター図では、各種差異(予算差異、操業度差異、能率差異)を求めることが課題です。
そのためには、まず直線の傾き=変動費率と固定費率 を求めます。
傾きが分かれば、Yの増分(=費用の差異)は、Xの増分(=操業度の差)に傾きを掛けることで計算できるからです。
例えば、上の図で操業度差異を求めるならば、
操業度差異=固定費率 ×(実際操業度 - 基準操業度)
で計算できます。
能率差異(変動費分)を求めるならば、
能率差異=変動費率 ×(基準操業度 - 実際操業度)
というように計算できるわけです。
固変分解(高低点法)
例題: 高低点法により、変動費率と固定費を計算しなさい。
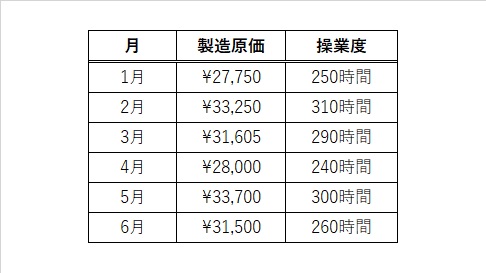
高低点法とは、原価を変動費と固定費に分ける方法のひとつです。
過去のデータのうち正常な範囲内にあるものの中から、操業度が一番高いときと一番低いときのデータ2点を選んで、変動費と固定費を計算します。
例題のケースでは、
操業度が一番高い ⇒ 2月の製造原価33,250円、操業度310時間、
操業度が一番低い ⇒ 4月の製造原価28,000円、操業度240時間
です。
製造原価と操業度との関係は、この2点を通る直線で決定される、と考えるわけです。
そしてこの直線の傾きが変動費率、切片が固定費になります。
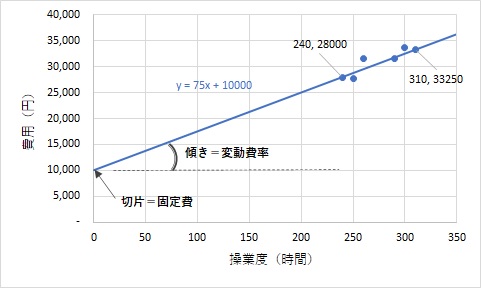
それでは、このグラフの傾きを求めてみましょう。
以下の2点を通る直線の傾きa を求めます。
(X1, Y1)=(240, 28000)
(X2, Y2)=(310, 33250)
a =(Yの増分)/(Xの増分)
=(Y2 - Y1)/(X2 - X1)
=(33250 - 28000)/(310 - 240)
= 75
次に、切片b を求めます。
傾き a = 75 なので、この直線は Y=75 × X + b と表せます。
この直線は(X1, Y1)=(310, 33250)の点を通るので、
33250 = 75 × 310 + b
となっているはずです。よって、
b = 33250 - 75 × 310
= 10000
と求めることができます。
(X2, Y2)=(240, 28000)の点を通ると考えても同じ結果になります。
28000 = 75 × 240 + b
b = 28000 - 75 × 240 = 10000
どちらの点で計算しても同じ結果になることがわかりました。
直線の傾きが 75、切片が 10000 と求まりました。
よって、変動費率は 75円/時間、固定費は 10,000円となります。
まとめ
いかがでしたでしょうか。
一次関数とそのグラフについてまとめてみました。
一次関数の特徴は、「傾き」と「切片」です。この特徴を理解すれば、
工業簿記における変動費率⇒傾き、固定費⇒切片 となることがわかると思います。
参考になれば幸いです(^^)
